From Symbol Manipulation to Meaning Making
Video Resources for Mathematics and Science Students
The team collaborated to develop videos for five subject themes:
mathematics, physics, chemistry, biology and current research.
Within each theme are four rate of change subtopics:
meaning of terms in differential equations, average versus instantaneous rate of change and sign, moving between graphical representations, and integration as accumulation.
Navigate down the columns above to see all the videos on one theme (e.g. physics).
Navigate across a row to see all the videos for one subtopic (e.g. average versus instantaneous rate and sign).
mathematics, physics, chemistry, biology and current research.
Within each theme are four rate of change subtopics:
meaning of terms in differential equations, average versus instantaneous rate of change and sign, moving between graphical representations, and integration as accumulation.
Navigate down the columns above to see all the videos on one theme (e.g. physics).
Navigate across a row to see all the videos for one subtopic (e.g. average versus instantaneous rate and sign).
Differential Equations: Meaning of Terms
Understanding differential equations entails paying close attention to the various terms and recognizing the meaning of each. Potential pitfalls include confusing parameters with initial conditions and failing to recognize the relationship between the underlying function and its first and second derivative. The videos explain initial conditions in differential equations (mathematics), and explore motion along two axes in a ball toss (physics), the order of chemical reactions (chemistry), the basic parameters of population growth (biology), and the clearance of medications from the blood (current research).
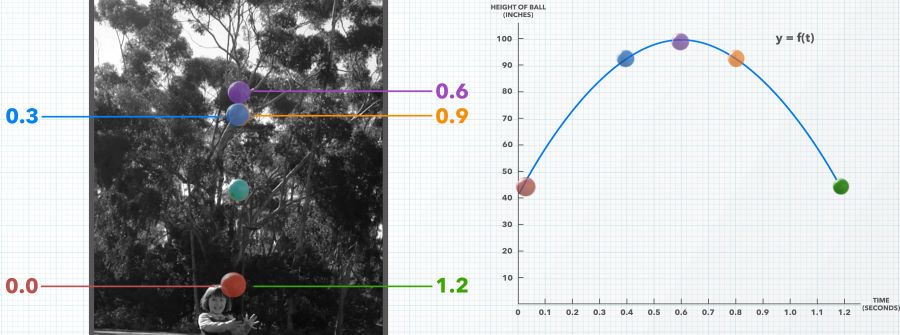
Average Versus Instantaneous Rate of Change and Sign
Understanding rate of change requires attention to both the magnitude of absolute value of the slope and the sign of the rate of change simultaneously. Initial, instantaneous and average rate of change must be distinguished symbolically, on graphs and using appropriate calculations for each. Learners may master the calculations but still struggle to explain what is happening in words. The videos explore average versus instantaneous rate and sign in a horizontal ball toss (mathematics), running on a track (physics), the chemical reactions of a hydrogen car (chemistry), yeast fermentation in bread (biology), and the separation of RNA molecules on a gel (current research).
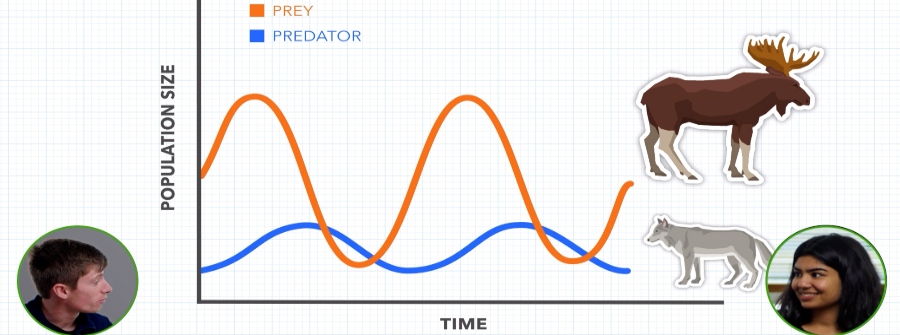
Moving Among Graphical Representations
Fluency with graphical representations entails being able to glean information from different kinds of graphs by plotting the same data in different ways, as well as being able to move between the graph of a function and the graph of its first and second derivative. In the videos, scenarios about water in rain barrels (mathematics), a mass on a spring (physics), tie dye shirts (chemistry), populations of wolves and moose (biology), and stellar flares (current research) illustrate the usefulness of fluency with representations and help make it more intuitive.
Relationship Between Rate and Accumulation
A core principle in calculus (the fundamental theorem of calculus) is that the accumulation of a quantity (determined by integration) and the rate of change in the accumulation of the quantity (determined by differentiation) are interrelated. It is common for learners to confound “amount” and “rate of change of amount,” and to fail to recognize the relationship between integration and the area under a graph. To explore these relationships, travel, rotation and more (mathematics), skateboarding (physics), gas chromatography (chemistry), cell cycles and flow cytometry (biology) and the fate of pharmacological substances in the body (current research) are topics explored in the videos.
